Erosional Processes in Catchment Areas and Methods of
Prediction and Protection
Introduction
The surfaces of catchment’s areas, subject to erosion during rainy seasons and thaws, are the principal sources of river-polluting drifts. The harmful impact of erosion is not limited to the damage inflicted only on agriculture. Erosion inflicts substantial damage on the water-economy and recreational resources.
Erosion due to thawed snow has been thoroughly studied by M.S. Kuznetsov with his associates and followers [4], while river-bed erosion by R.S. Chalov and co-workers. With enviable skill and great love, Chalov, in his publications, shows how important for the progress of science is the legacy of such predecessors as N.I. Makkaveev was.
The tendency to closer quantitative mathematical description of individual processes of erosion led to the development of prediction problems in the non-classical statement, at scientific centres of the former Soviet Union, if classical is reserved for the USLE method that was usefully applied in the US and other countries for over 50 years [22.26.28].
Development
of methods of prediction of soil scour
Mankind has sought to work out fairly precise methods
of predicting soil scour since the very
first days of civilization. However, work on this has become more purposeful
since the time of organization of the service of soil protection in the
Notwithstanding the importance of quantitative methods of prediction of erosional processes for the solution of applied tasks, for many years the theory of soil erosion has, unfortunately, been fettered by verbal qualitative assessment. Sufficiently reliable methods of quantitative estimation and of predicting individual stages were non-existent.
The methodology presented to the 3rd Hydrological Congress in 1957, devoted to analytical determination of non-scouring velocities for cohesive soils, is considered to have been the date of emergence of analytical methods of quantitative estimation of soil erosion [4]. The methodology just cited took fairly full account of the physico-mechanical properties of soils and the hydromechanical parameters of flow, in contrast to the hitherto existing method based on the qualitative assessment of only soil types. The prior importance of this approach lies not so much in its potentialities of quantitative determination of the non-scouring velocity for cohesive soils according to the actual physico-mechanical characteristics of resistance to scour and in initiating a number of studies but also – as pointed out by K.V. Grishanin [1] – “in reflecting the probabilistic character of the start of movement of soil particles”. And this process, as Albert Einstein noted in a conversation with his son, “is too complex”. [27].
Further, with the aid of one of the major indices of hydrology and mechanics of liquids (of the non-scouring velocity of a water flow), in the 1960s an equation of soil scour, based on the fatigue theory of separation of aggregates, was derived with the aid of the laws of mechanics [5]. Fatigue implies loosening of the links of aggregates with the soil mass under dynamic impact of the pulsating slope runoff.
The equation for predicting soil scour in the course of time I has the form:
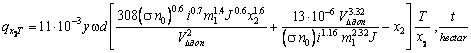(1)
where g
is the volume weight of soils under full water saturation, t/m3; d is the average size of aggregates (separating particles), VDperm is the permissible near-bed non-scour (non-eroding) velocity of flow
of the water stream; w is the mean frequency of pulsation velocity. It may be determined
by the Strouhal number 
(V
is the mean velocity of slope runoff, H is the depth of runoff). In the absence of data of special
studies the value of w is assumed to equal 10 l/sec.
J is the average intensity of precipitation m/sec; T is the duration of excessive rainfall or the time in the course of which the layer of precipitation exceeds that of infiltration; s is the coefficient of runoff; no is the coefficient of hydraulic resistance (Manning coefficient); i is the average slope of surface, equal to the ratio of the difference of the levels of the contour interval of the slope according to A.N. Kostyakov [9, 13], coefficient describing the roughness of the slope surface, the concentration of runoff ; x is the distance from the watershed to the end of the eroded part of the slope; m1 is the coefficient of the deviation of the character of movement of the slope runoff from that assumed in the calculation scheme of the movement of an equal layer of water.
Equation (1) – called ‘hydromechanical’ in the literature – at verification, shows a fairly satisfactory agreement with observation data. Notwithstanding its considerable age, the formula remains competitive to the present day. This property is due to its being simple to master and apply – its potentialities of constant perfection. However, further analysis points to the need of some specification. After all, it is sometimes useful to complicate the theory in order to reflect the real situation of the process more correctly and precisely than to use too idealized assumptions.
On the basis of [6], the curve of ‘fatigue’ strength may be approximatively expressed by the dependence:
(2)
where 
is the number of
stress cycles; 
and 
are the breaking
stress respectively at the initial and final moments of load impact; 
is the dimensionless
coefficient depending on the characteristics of flow and properties of soils
under erosion, 
, then
(21)
The term ‘fatigue’ is applicable in explaining the breakdown of links as a result of the action of cycle loads over a certain period of time. Dynamic loads on the bed are due to the near bottom velocities of water flow at the initial and final moments of deformation VDi and VDf; the latter, at full stabilization, is equal to the permissible non-scouring near-bottom velocity VDb. In expressing the stress of aggregate detachment through these velocities, the dependence (1) assumes the form:
(3)
When the average frequency of pulsation velocities w is known, the time needed for the detachment of a particle may be determined.
(4)
Consequently, the number of particles detached from a section l´l over one second will total:
(5)
where V is the mean velocity of flow, H is its depth.
It would probably be more correct if the numerator of the formula (3) were also a measurable value, e.g. one most fully characterizing erosion by erosion resistance, i.e., by permissible non-scouring flow velocities. These indices may be determined with fair precision, depending on the flow parameter and soil properties. In the dynamics of river-bed flow [6, 8] fairly well-grounded expressions are available for calculating this widely applied parameter, and a standard has been developed.
The way of forced (accelerated) tests of soil scour, proposed by the author [10], appears to be most acceptable for determining the type of ‘fatigue’ curve and for calculating the parameter N in the formula (3). In the experiments on accelerated testing of scour the value of the near-bottom scouring velocity of flow VD, the duration of time prior to scour (mass detachment of particles rather than detachment of an accidental loosely-linked aggregate) τ and the depth of flow are recorded.
The sought values are determined
from the equation (4), solving it relatively to N *:
(6)
As shown by the results of forced (accelerated) tests of soil scour, the value of N * often differed from the values calculated by the formula (4): N *=188000. Such a value corresponds to soils characterized by permissible (non-scouring) velocities (VDperm = 0.12÷0.13 m/s); with an increase of permissible velocities this index grows.
The results of numerous experiments on accelerated
testing of soil scour of varying composition, provenance and geographic
location (hundreds of samples of soils of intact composition have been tested from the route of the main canal Siberia –
Middle Asia) have enabled to find the function of N *= f(VDgen), where N *
has been calculated by the dependence (4), when the experimental values of VDperm, VDx are known.
Approximation of he curve allowed to obtain a formula for determining the coefficient of N *, depending on the erosional resistance of soils expressed by the most important index, namely the permissible (non-scouring) velocity of flow, which reflects both the resistance of soils to erosion and the value of the non-silting velocity of flow:
(7)
(8)
It should be noted that the above analysis of the
results of studies is not definite, and may be made more precise in the course
of emergence of more detailed data. As is known [5], the number of detached
aggregates from a 1´1 plot per second totalled 
.
Substituting the value of N from formula (8) in the expression n1 we obtain:
(9)
At the time of stabilization of scour the value of the acting near-bottom velocity approximates the permissible (non-scouring) near-bottom velocities. Practically, erosion ceases when the near-bottom velocity of surface runoff VDx»1.15VDperm.
Substituting the value n1 in (1) and taking into account the experimental data, as well as the fact that the number of aggregates of d size per unit of the width of the river-bed m2=α2/d, an expression of silt at uniform movement of flow:
(10)
For the discharge of silt at a site at the distance 
from the origin of the
watershed, under the known averaged value of the near-bottom velocity at the interval 
, the expression will assume the form:
(11)
The total discharge of silt per unit of time from an
area on a slope, whose length is 
, while the width equals unity, may be determined by
integrating the expression (11) between 
and .
The earlier dependence [4.8] proves valid for the
condition 
m/s:
In case it proves unfeasible to integrate the expression for VDx, the total discharge of silt is obtained by final summation or graphically.
Active erosion will last until the saturation of the slope runoff reaches the limiting transporting capacity. If we designate the distance from the watershed to this point x1, the length of the section of active erosion will total [4]:
, (12)
while the length of the accumulation section at the slope length :
, (13)
Substituting the value VDx=VDperm in the equation (11), we shall obtain the length of the non-eroding section of the slope:
(14)
where the coefficient 
varies from 1 to 3; at
transverse ploughing its value is less than at longitudinal ploughing.
If the coefficient of pressure loss is expressed through the height of roughness protuberances according to V.N. Goncharov –no=D1/16/22.2 [4], we shall obtain:
(15)
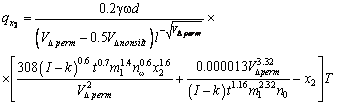(16)
and the value of the soil scour (t/ha)
(17)
In the absence of results of special studies, necessary for determining the non-eroding (non-scouring) velocities of water flow, use may be made of the approach presented in [5].
An updated methodology enables a further consideration of the factors conditioning erosion, and a better-substantiated prediction of soil scour. The method may be used for ecological grounding of nature protection measures aimed at minimization or prevention of erosional processes.
The derived modified method of calculating soil scour permits a more adequate description of individual stages of erosional processes of soils.
Notwithstanding the above-said, experience of solving
analogous tasks suggests that complex models should be avoided,
no matter how elegant they may be. Reasonably approximative
solution of a problem should be considered acceptable. Such models merit
preference, for they permit measurement of the parameters involved in the
expressions. One should not be oblivious of the fact that it is not only the
models that err but input data as well, which are very often very difficult to
determine with prescribed precision. The precision of input data has a poor
reputation in connection with their errors. Problems exist also in the methods
of measurement and in the devices themselves. Therefore, one should not expect
the models being created, no matter how perfect, to yield precise results. In
this connection interest attaches to the
statement made by the American Robert Aumani, winner
of the Nobel Prize, to the effect that “Scientific theories may be judged by
how well they allow to organize our observations”. Of course, one should reject
outright the temptation to solve a task purely empirically, because of the
well-known shortcomings. Hence, the proposed specifications ought to be used
only for highly responsible items.
Under the present status of the study of the erosional process, it seems to be more important to concentrate the basic thrust of investigations on the solution of tasks that allow to take timely adequate measures in order that calmly proceeding erosional processes do not develop into landslides, mudflows or – at long-term neglect – into desertification [13]. To this end, timely assessment of the hazard and vulnerability of the onset of erosion of impermissible limits, leading to the formation of deserts, appears to be of primary importance [15].
Therefore, perfection of the prediction of soil scour is not restricted to the progress and status of study of soil erosion. Intensive search for fresh ideas is necessary, primarily of measures for preventing the onset of erosion, search for the harbingers of a critical situation, based on a prediction in advance of the hazardous state and vulnerability of slopes.
On the
Hazardous State under Erosion
In view of the clearly expressed random character of the factors conditioning the erosional process, the need assumed priority of applying the methods of the probability theory, theory of random processes, reliability theory and of risk analysis in solving tasks connected with erosional and channel processes conditioned by a multiplicity of interconnected variables or random factors.
Use of combined solutions of the equations of the Japanese mathematician Keiso Ito and those of Fokker-Planck-Kolmogorov [18], applied in [11, 15] with fair success in solving various tasks connected with degradation, proved fruitful. As a matter of fact, the proposed stochastic model seeks to correlate two variables in terms of their functional probability rather than simply using regression by the method of least squares.
These characteristics enable to assess in full measure the impending hazard and to map out more effectively an optimum sequence of measures towards averting or mitigating the damage from these crisis situations linked with the uncontrollable elements.
Methods used in assessing the critical state of erosion, often based on a verbal evaluation of the state by (ordered) linguistic scales, are undoubtedly simple and convenient. However, it is hard to use them for reliable final numerical calculations indicating the probability of onset of this event; at the same time, humans usually find it difficult to subjectively identify many stages (the limit is ten or twelve stages). Neither the use for this purpose of extrapolation and expert evaluations can be considered to be in line with the modern level of development of contiguous sciences whose techniques may be used to predict the time (moment) of the emergence of critical situations.
The tasks set may be solved by empirical and analytical methods. Empirical methods suffer from well-known shortcomings. At the same time, it is very difficult to analytically describe the hazardous state of soils under erosion precisely or with prescribed precision, with account of the time of its emergence. Hence, creation of models, at least approximatively answering the tasks set and allowing to take measures of prevention, ought to be considered urgent.
The proposed methodology of hazard assessment and the
strategy of soil protection, developed on its basis, will not allow development
of soil erosion of high and catastrophic intensity, attended by landslips,
mudflows, desertification and other disasters linked with the uncurbed
elements.
Theoretically, any impact on the soil cover brings
about its weakening or degradation to some extent. However, in practice it is
important to know the value of an impact
causing breakdown (erosion) above permissible limits and inflicting substantially
greater damage than inevitable erosion within permissible limits [13, 14, 24].
As evidenced in practice, it is highly difficult to successfully solve the problem of foreseeing individual stages of the life cycle of soil cover under erosion, demanding the consideration of a very large number of variables or indeterminate parameters from positions of the traditional deterministic approach. It will be recalled that this approach may be considered to be a purely private type of a much more general – probabilistic – approach.
In analysing the erosional process and the hazards of its development into a disaster, it is easy to come to the conclusion that, notwithstanding the fairly high level of development of the science of erosion, cumulating the findings of researchers of many generations [1, 3-15, 19-28], it is impossible, in assessing the onset of a hazardous state, to avoid errors caused by the use of averaged data. The methods of assessment of the hazard of erosion, used at present, lag behind the modern level of development of the reliability theory. Meanwhile, it is on the basis of this theory that the limiting state of many complex systems is assessed at present [7, 11].
An analysis of the functioning of soil cover [8, 12] and analogous systems, as well as literature data, points to the fact that there is no limitation (ban) on the use of principles underlying the determination of the indices of reliability for these items. There is much in common between their functioning [7, 12-16]. The approaches of the reliability theory play an ever increasing part in modern natural science, for they allow to represent the functioning of one or another living or non-living system in quantitative and comparable form and, in principle, they may be represented by one and the same mathematical expression [7, 11-15].
Definite experience has accumulated at the
The noted merits of this vitally important sphere of knowledge, research on which was first commenced in the former USSR, including in the assessment of soil stability under erosion [9, 23], and further winning recognition in foreign countries, have prompted the author to consider it feasible and prospective to use methods of the reliability theory – adapted for the solution of the task in hand – for the assessment and description of hazardous states at erosion.
Analytical
Evaluation of the Time of Onset of the Hazardous State of Soil
To solve the task set, one must primarily select the model of functioning and to form the criteria (prognostic variables) towards which the assessment of the hazardous state of the soil cover under erosion should be oriented – in relation to which the environment under discussion is being analyzed. The prognostic variable, selected for the solution of the task, should have sufficient sensitivity to the change of the main among the basic factors making for the functioning of the soil system. The intensity of erosion and the change of this intensity over time should be considered to be the most characteristic indicator for the description of hazardous situations. To this end use may be made of the laws of distribution of Humbel’s extreme values, Poisson’s random events, as well as the theorem of conditional probability, theorem of hypotheses, the Bayesian approach, etc. [7-16, 23-25].
To choose the distribution it is important to check the agreement of experimental with theoretical distribution through a computer analysis of the distribution of statistics, which is not difficult either in principle or in practice.
The state of soil systems under erosion is conditioned by a large number or random – frequently indeterminate – factors. Therefore, in analysing and deriving expressions, describing the process, in the first place consideration should be given to the statistical, random nature of the change of the system, and the variable character of the course of biological, physical and other processes. Looking for analogies between well-studied physical processes and the ‘vital functions’ of the systems under study, many common features can be found between them, especially when examining the principal cause of changes or degradation.
As shown by an analysis of the potentialities of various methods, those of Markov processes appear to be most suitable and effective for an approximate solution of the task set, involving the description of variable random processes of the functioning of a system [18]. In particular, this implies application of stochastic kinetic equations used in physics to study diffusional and other analogous processes. They may be assumed to be described by one and the same equations of diffusion processes by which Brownian movement is described [17, 18]. The Markov process – widely used in practice – is a special type of random processes. Thus, e.g. radioactive decay is described by the Markov process, at which the probability of the disintegration of an atom over a small span of time does not depend on the course of the process in the preceding period.
An important characteristic of the value of remoteness of the prognostic variable from the limiting state brought about by the degradation process may be determined with the aid of a differential stochastic equation, first proposed by K. Ito [17, 18] to solve problems connected with diffusional processes
(18)
where y(t) is the prognostic variable, m(t) is the mean velocity of change of the prognostic variable; s(t) is deviation of the mean velocity of change of the prognostic variable or coefficient of diffusion; x(t) is a Gauss-type random constituent.
The task of analysis is to determine the time until the first crossing by the processes (18) of the upper limit of the area. The problem may be solved if the conditional density of the probability of the transition of the process from one state to another is known. The conditional transitional density for a Markov diffusion process is usually described by the Fokker-Planck-Kolmogorov equation [17, 18]. Since the degradation process is due to continuous external action, the change of the character of the random process may be fairly correctly taken for monotone. A monotone process physically implies an assumption on the irreversibility of the accumulating damage. In solving the problem, considering the process under study monotone with constant mean velocity of change of the prognostic variable, as well as with constant standard deviation, the equation (18) may be expressed
. (19)
The equation (19), describing the change of the prognostic variable, leads to a diffusional distribution of the time of failure-free functioning, whose type is determined by a relevant solution of the Fokker-Planck-Kolmogorov equation [17, 18]. Prior to its rigorous derivation by A.N. Kolmogorov, this equation occurred earlier in the works of the physicists Fokker and Planck, hence it is often called Fokker-Planck equation
(20)
When the realization of the process (19) has a monotone character, the boundary conditions may have the form [17, 18]
, (21)
, (22)
where d(y) is the delta-function.
The solution of the equation (20) with conditions (21) and (22) is known as a fundamental solution of the equation (20), assuming the form:
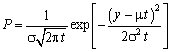. (23)
The density of the time distribution of the first reaching the prescribed threshold by the process has the form
(24)
where α is the limiting (threshold) value of the prognostic variable, at reaching which failure sets in.
An analysis of the process under study shows that the first crossing by the process described by the equation (19) of a certain determined boundary – the limiting value of parameter α, at which a critical, hazardous state sets in, should be considered the beginning of the onset of hazardous state. After simple transformations, with the process being monotone, the distribution function of time of the first reaching the prescribed boundary by the process (19) will have the form
(25)
The probability of the onset of the limiting state (failure situation) may be expressed thus
(26)
The mathematical expectation and dispersion of the time of failure-free functioning is determined by the expressions.
Using the parameter Z, which is a normalized normally distributed random value (statistical margin of resistance), the expression (26) may be re-written thus:
. (27)
Raising the expression (32) to the square and solving the quadratic equation relative to t, we obtain
. (28)
Consequently, the time (moment) of the onset of the hazardous state t is represented by the expression
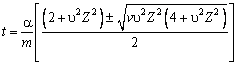, (29)
where 
is the variation
coefficient.
Assessment
of the Risk of Breakdown of the Soil Cover and on taking Anti-erosional
Measures
In order to avert the risk of hazardous state of the soil cover under erosion and to protect soils from these degradation processes a number of antierosional protective measures should be taken. In terms of the reliability theory these measures may be considered reservation [7, 25].
Rational planning of measures of anti-erosional protection calls for the identification of all possible hazardous situations and selection of adequate measures for their removal or mitigation. Anticipating hazardous situations, it is important – on the basis of probabilistic analysis – to estimate the numerical value of safe functioning of the slope under cultivation, taking account of all measures of protection against erosion, as well as of all types of anticipated hazards that may arise at reclamation of the slope.
Dividing the time of functioning of the item into intervals 
, the probability of safe functioning of the eroded slope may
be described by the expression
(30)
where 
is the probability of
prevention of hazardous situations as a result of measures mapped out towards
the removal of hazardous situations in the time interval 
. The risk of emergence of a hazardous state will be
. (31)
Two states of erosion may be observed on a slope subject to erosion: permissible and impermissible. The state of slope under erosion, characterized by damage exceeding permissible limits, will be impermissible. Impermissible damage is one, the excess of whose value leads to an impermissible loss of the quality of the slope, in consequence of which its purposeful use is unfeasible. Obviously, the sum of probabilities as incompatible events – of permissible Pperm and impermissible state rimp totals unity.
. (32)
The usefulness of joint study by representatives of different schools is a new method of calculation of the distance between anti-erosional earth banks, taking fuller account of hydromechanical parameters and soil resistance to erosion, carried out jointly with the well known British specialist Roy Morgan [21].
The method of designing and building antierosional hydrotechnical structures and the methods of their calculation, with maximally fuller account of the factors making for the reliability and length of service of these items, set out in [10], is worthy of attention [16]
Notwithstanding the urgent need, literature on hydrotechnical antierosional structures is very scarce. This considerable gap has been removed by the creation and publication of the monograph [16].
Considering on the whole the development of the
science of soil erosion here – in the former
Finally, I would like to explain to those to whom it may seem that too much attention is given in the paper to methods of predicting hazards and vulnerability at the expense of other details of studying erosional processes and the damage they cause. This is only because the basic difficulties awaiting us in the future will be precisely these forerunners of erosion and much depends on their timely prediction for soil protection.
In conclusion, stressing the exceptional importance of investigations on the given problem, it should be noted that considerable improvement in the state of soil resources may be attained by stimulating investigations in a number of priority directions, the list and substantiation of which are presented in the author’s monographs [13, 16]. However, it should not be forgotten that the problem in the future will lie not only in carrying out studies as such but in linking the findings of studies to processes of decision-making.
If the results of studies, carried out in one of the
leading centres of the former
References
1. Grishanin K.V. The channel process. M. Transport, 1972. 215 p.
2. Kirkby M.J., Morgan R. Soil
erosion, M. Kolos,
1984. 415 p.
3. Kuznetsov M.S., Glazunov
G.P. Erosion end protection of soils, M.: MSU Publishers, 1985. 334 p.
4. Mirtskhoulava Ts.E.
On the process of bed scour in cohesive soils // Paper presented at the 3rd
All-Union Hydrological Congress. Proc. GGI. 1957. pp. 53-54.
5. Mirtskhoulava Ts.E.
Engineering methods of calculating the prediction of water erosion, M. Kolos, 1970.
239 p.
6. Mirtskhoulava Ts.E. Some modern problems of the mechanics of erosion and
their solution from the probabilistic standpoint, L. Gidrometeoizdat.
7. Mirtskhoulava Ts.E.
Reliability of water reclamation structures. M, Kolos, 1977. 280 p.
8. Mirtskhoulava Ts.E.
Methodological recommendations on the prediction of water (rain) erosion of
soils, M. Vaskhnil,
1978. 61 p.
9. Mirtskhoulava Ts.E.
The principle and calculation of the reliability indices of the soil cover //Georgian Sci. Res. Inst. Hydrol.
and Recl. 1986.
pp. 48-61.
10. Mirtskhoulava Ts.E.
The basics of the physics and mechanics of channel erosion. L. Gidrometeoizdat, 1988.
326p.
11. Mirtskhoulava Ts.E.
Ecological disturbances,
12. Mirtskhoulava Ts.E.
New potentialities of assessing soil quality //Pochvovedenie, 1998. N6. pp. 727-731.
13. Mirtskhoulava Ts.E.
Soil Erosion,
14. Mirtskhoulava Ts.E.
On limiting permissible losses of soil under erosion // Pochvovedenie, 2001. N3.
422p.
15. Mirtskhoulava Ts.E.
Soil degradation and ways of predicting the onset of unfavourable state // Pochvovedenie, 2001. N8, pp. 712-716.
16. Mirtskhoulava Ts.E. Anti-erosional hydrotechnical structures.
17. Pogrebenski S.B., Strelnikov
V.P. Design and reliability of multiprocessor digital computers. M. Radio i svyaz,
1988. 168 p.
18. Tikhonov V.I., Mironov
M.P. Markov processes. M. Sovetskoe radio, 1977. 416 p.
Chalov R.S. Geographical investigations of channel processes. MSU Publishers, 1979. 214 p.